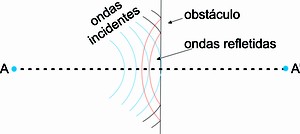
Como citado anteriormente, os fenômenos que serão verificados dentro de um tubo de Kundt são as ondas estacionárias. Elas ocorrem quando
uma onda é sobreposta por ela mesma por ter sido refletida em uma
superfície, o que faz ela voltar com sentido inverso. Este fenômeno pode
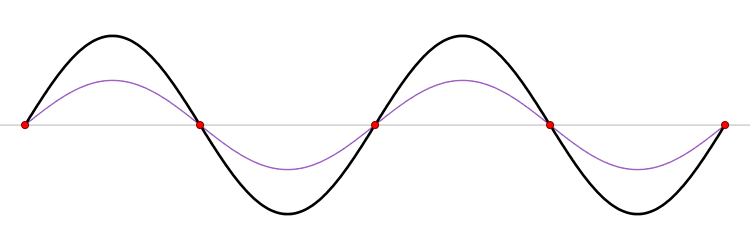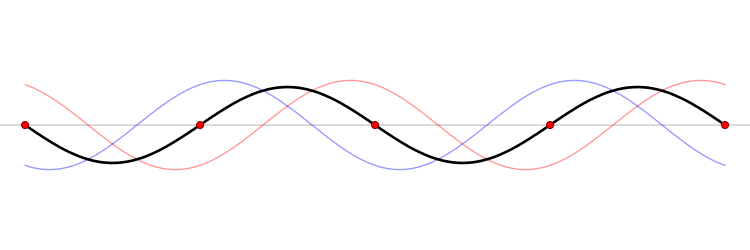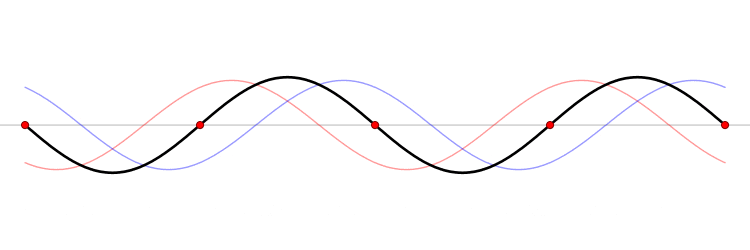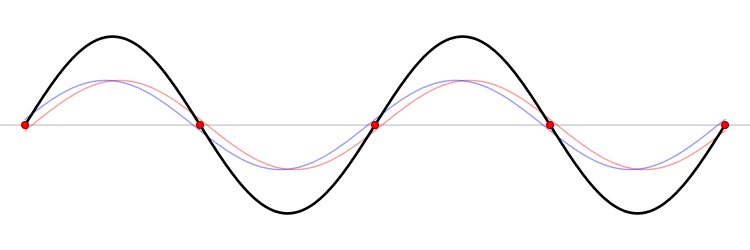
ser observado na imagem animada abaixo (Figura 1).
Figura 1. As ondas azul e vermelha são, respectivamente, as ondas gerada e refletida. Já a preta é a representação da interferência entre as outras duas.
Fonte: Giphy. Disponível em: <https://giphy.com/gifs/wave-waves-form-cH5qB4vqM8NoI/>
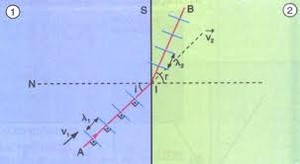
As ondas estacionárias possuem alguns elementos que precisam de alguma análise. Como é possível perceber, ainda na figura acima, existem momentos em que ambas as ondas (azul e vermelha) se sobrepõem sem diferença alguma de fase, ou seja, ficam literalmente sobrepostas, a representação de suas interferências passa a possuir uma amplitude maior (interferência construtiva), o nome dado a esta área é ventre. Podemos perceber também, ainda na Figura 1, que quando as ondas se sobrepões com amplitudes opostas, a representação de suas interferências é nula (interferência destrutiva), o nome dado a esta área é nó. A Figura 2, abaixo, demonstra esta aplicação em ondas estacionárias.
Figura 2. Representação de uma onda estacionária onde "λ" é o comprimento de onda, "V" são os ventres e "N" são os nós.
Fonte: Domiciano Correa Marques da Silva. Disponível em: <http://brasilescola.uol.com.br/fisica/ondas-estacionarias.htm>
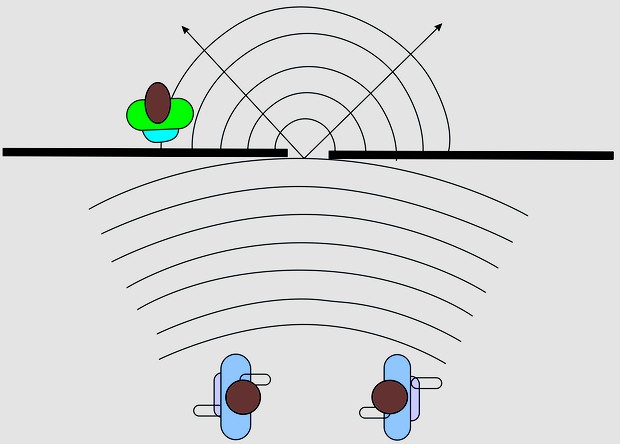
Outro elemento pertencente as ondas estacionárias são os harmônicos, que nada mais são que a distância entre dois nós. É possível perceber também que existe uma relação entre número de harmônicos (n) e comprimento de onda (λ), onde "λ" é igual a metade de "n", a Figura 3, abaixo, traz estas representações. Vale salientar que, no tubo de kundt, o material utilizado para visualizar as ondas (no caso deste projeto, bolinhas de isopor) ficará concentrado nos locais onde não existe transmissão de energia, ou seja, entre os harmônicos.
Figura 3. Representação dos harmônicos em uma onda estacionária.
Fonte: Anderson Guimarães Guedes. Disponível em: <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S1806-11172015000200017>
Em reuniões realizadas com professor orientador foi-nos passado que o objetivo deste projeto seria, a partir da observação do tubo de kundt e do cálculo necessário, responder a ele qual a frequência que foi posta no gerador de frequência, onde foi-nos passado as seguintes equações, lembrando que o meio no qual as ondas sonoras irão se propagar é o ar.
Equação 1. Equação da velocidade de uma onda que relaciona o comprimento e a frequência da onda.
onde v = velocidade; λ = comprimento de onda; f = frequência.
Equação 2. Equação da velocidade de uma onda que relaciona as Equações 1 e 2.
onde v = velocidade; B = módulo de elasticidade do ar; ρ = densidade do ar.
Desta forma, como ambas as equações determinam a velocidade, podemos iguala-las, o que nos dará a equação a seguir.
Equação 3. Equação da velocidade de uma onda que relaciona as Equações 1 e 2.
Ou seja, temos que a raiz do módulo de elasticidade do ar sobre a densidade do ar é igual ao comprimento da onda multiplicado pela frequência da mesma. Os valores de módulo de elasticidade e densidade do ar são tabelados e o comprimento da onda pode ser obtido a partir da relação, citada anteriormente, existente entre número de harmônicos e comprimento de onda, sendo assim, como pode ser visto abaixo, teremos como equação final, deixando a frequência isolada, o seguinte.
Equação 4. Equação 3 após o isolamento da frequência.
Referências:
HALLIDAY, D.; RESNICK, R. Fundamentos da Física - Gravitação, Ondas e Termodinâmica. 9ª ed. Rio de Janeiro: LTC, vol.2, 2012